OBJETIVOS
OBJETIVO GENERAL
Determinar experimentalmente la difusividad térmica de un líquido
OBJETIVO PARTICULAR
Discutir la importancia de los mecanismos de transferencia de calor
Comprender que la transferencia de calor se puede llevar a cabo en varias direcciones y en régimen no estacionario
INTRODUCCIÓN
Todo el estudio de la transmisión de calor corresponde a la Termodinámica de la evolución y no a la Termodinámica del equilibrio, pues el interés se centra aquí no ya en cuánto calor se transmite, sino en determinar a qué velocidad fluye éste.
Lo que se estudia aquí no es el calor intercambiado entre dos estados sino el flujo temporal de calor por unidad de área de paso.
La transmisión de calor es el flujo de energía térmica y siempre va asociado a una diferencia de temperaturas. Tradicionalmente se acostumbra a distinguir tres fenómenos básicos para la transmisión de calor: conducción, convección y radiación térmica.
El análisis de la transferencia de calor de un estado transitorio se parte de la ecuación general de conducción de calor o también llamada Ley de Fourier, con variables tales como son: conductividad térmica (k), difusividad térmica (α), tiempo adimensional (τ), temperatura adimensional (θ), etc.
La difusividad térmica del material representa físicamente la rapidez con la que se difunde el calor a través del material al estar en contacto con otro. Por lo tanto, cuanto mayor sea el valor de α, mas alto es el ritmo de calor en el material. El valor elevado de α es el resultado de un alto valor de conductividad térmica, que indica una elevada rapidez de transferencia de energía o de un valor bajo de capacidad calorífica.
Para determinar α existe la siguiente ecuación:Donde:
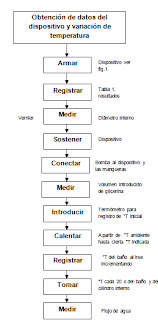
DESARROLLO EXPERIMENTAL
Fig. 1 Arreglo experimental para la determinación de difusividad térmica
RESULTADOS
Tabla 1. Cambio en el la temperatura del líquido problema (glicerina) y en la variación de la temperatura del líquido de enfriamiento (agua).
Tabla 2. Valores de Ɵ (Temperatura adimensional) obtenidos a partir de los datos resaltados de la Tabla 1.
Tabla 3. Valores de tiempo adimensional y de difusividad térmica obtenidas a partir de los datos de la tabla 2.
Tabla 4. Resultados generales obtenidos
Tabla 5. Mediciones de flujo del líquido de enfriamiento
Figura 2. Perfiles de temperatura para la conducción de calor en régimen no estacionario en un cilindro. T0 es la temperatura inicial del cilindro y T1 es la temperatura de la superficie para t>0. Obtenida de Bird, et. al., 2006, pág. 11-6.
ANÁLISIS DE RESULTADOS.
De la tabla 1 se consideraron sólo los datos marcados que están entre 37.9 y 38.2 °C para el líquido de enfriamiento porque la glicerina nunca llegó a más de 38.2 °C y tenía que estar en un intervalo pequeño pues en principio la temperatura del líquido de enfriamiento se debía mantener constante lo cuál fue difícil lograr porque el equipo no tenía un sistema de regulación automático de temperatura.
Para conocer los valores de temperatura adimensional se hicieron interpolaciones lineales entre las dos rectas que se rodeaban al punto de tiempo adimensional deseado (véase Memoria de cálculos). Para valores de tiempo adimensional mayores a 0.84 no era posible hacer interpolaciones pues no había una curva encima de ese valor así que se consideró una curva imaginaria con valor de tiempo adimensional de 0.6 y temperatura adimensional de interesección de 1.0.
Por último, se sacó un promedio de difusividad α cuyo valor se da en la tabla 4. Se nota una importante desviación con respecto al valor de difusividad teórica de la glicerina de un 710%. Un error de esa magnitud se explica porque 7 de 16 valores de Ɵ considerados estaban encima de 0.84 y como ya se dijo anteriormente, se propuso una curva imaginaria con un valor de 0.6 del cual no se tiene certeza alguna. Además, se suponía que ni el flujo ni la temperatura del liquido de enfriamiento debían cambiar con el tiempo, que era un sistema aislado y que el glicerol era de calidad analítica, supuestos de los que no se tiene certeza de haber cumplido.
CONCLUSIONES
La medición de la difusividad de glicerina de esta experiencia, aunque tuvo un error bastante amplio, es un buen resultado después de considerar que no era un sistema cerrado donde se medía la difusividad y las variaciones de temperatura del líquido de enfriamiento.
La difusividad térmica es un parámetro de suma importancia en la industria farmacéutica porque de éste depende la selección del tipo de material, velocidad de flujo, temperatura de circulación del fluido de enfriamiento y del tipo de biorreactor preferible a utilizar en procesos fermentativos. En la industria alimentaria también tiene un papel importante en la selección de los parámetros antes mencionados para los procesos de pasteurización.
BIBLIOGRAFÍA
-Bird, R., Stewart, W. y Lightfoot (2006). Fenómenos de transporte (1ª ed.). México, D. F.: Editorial Reverté
-Cengel, Y. y Boles, M. (2006). Termodinámica (6ª ed.). México, D. F.: Editorial McGraw-Hill.
-Chang, R. (2008). Fisicoquímica (3ª ed.). E. U. A.: McGraw-Hill
-Chang, R. (2010). Química (10ª ed.). E. U. A.: McGraw-Hill
-Petrucci, R., Harwood, W. y Herring, F. (2003). Química general (8ª ed.). Madrid, España: Pearson Educación
-Smith, J., Van Ness, H. y Abbott, M. (1997). Introducción a la termodinámica en ingeniería química (5ª ed.). México, D. F.: McGraw-Hill
-Welty, J.R. Fundamentos de transferencia de momento, calor y masa. Limusa, México 1972.
MEMORIA DE CÁLCULO
Cálculo de la temperatura adimensional Ɵ
Donde:
Ɵ=temperatura adimensional, °C/°C
T= temperatura de la glicerina en el tiempo, t, dado, °C
To=temperatura inicial de la glicerina, °C
T1=temperatura del líquido de calentamiento, agua, en el tiempo, t, dado, °C
Para el tiempo t=200 s, tenemos:
Cálculo del tiempo adimensional
Para calcular el tiempo adimensional se interpolaron los valores obtenidos de Ɵ en un valor de r/R=0 en la figura 2 y se obtuvieron los valores de Ƭ (tiempo adimensional).
Ɵ=temperatura adimensional obtenida en el paso anterior
Ɵinf= valor de Ɵ inferior de la gráfica que acota al valor de Ɵ dado
Ɵsup= valor de Ɵ superior de la gráfica que acota al valor de Ɵ dado
Ƭinf= valor de Ƭ inferior de la curva que acota el valor de Ɵ dado
Ƭsup= valor de Ƭ superior de la curva que acota el valor de Ɵ dado
Según esto, hay cuatro posibles formas de obtener el valor de Ƭ en el punto Ɵ buscado, dependiendo del valor de Ɵ.
Por ejemplo, para el valor de Ɵ encontrado en el punto anterior, tenemos:
Cálculo del valor de difusividad térmica α
α=difusividad térmica de la glicerina, m2/s
R= radio del cilindro desde el centro a la superficie, m
t= tiempo en el que transcurre el calentamiento, s
Para el valor de Ƭ encontrado en el punto anterior, tenemos un valor de difusividad térmica de:
"Poca ciencia aleja muchas veces de Dios, y
mucha ciencia conduce siempre a él"
Sir Francis Bacon













No hay comentarios:
Publicar un comentario
Deja tu comentario, puede ser anónimo. Todos son bienvenidos.